Farkle Kingdom Come Deliverance Best Strategy (Dice Games Chapter 2)

Farkle is a simple dice game in the video game Kingdom Come Deliverance. The aim is to reach 4000 points and the gameplay is kinda similar to dice blackjack. You start with 6 dice and you throw them. Certain dice have scoring value so you can put them aside and throw the rest of the dice again in hopes of scoring more points but if you don't get any scoring dice, you bust, i.e. "farkle". So it is smart to bank your points when you have too few dice left. Since farkle is an old game the scoring varies a lot. I decided to use the rules from the game Kingdom Come Deliverance. Here is the scoring:

-a single 1: 100 points

-a single 5: 50 points

-three of a kind: 100 points multiplied by the given number

-three 1's: 1000 points

-four or more of a kind: Double the points of three of a kind

-full straight 1 to 6: 1500 points

-partial straight 1 to 5: 500 points

-partial straight 2 to 6: 750 points

You can combine these scorings. So for example, if you were to get {1,1,2,2,2,4}, the two 1's would be worth $100+100=200$ points and three of a kind 2's would be worth $2 \times 100=200$ points. Then when you set aside the scoring dice, only one die is left. You can either choose to bank the 400 points or roll again with only one die. Let's say we were to roll it again. If that die was a 1 or a 5, i.e. a scoring die, when we set it aside we would get all the 6 dice back since there were no dice left. So we would roll again until we bank or farkle.

My Solution

Now that we've learned about the game, it's time to find the best strategy and then test it. But since some parts of the game are too complex, I decided to make life easy for myself.  You are always welcome to build upon my calculations. Maybe I'll make another post considering what I've left behind.

First of all, the strategy doesn't count in what the opponent's score is. Of course it makes more sense to roll once again when the opponent is 50 points away from winning. In my game the only aim is to get to 4000 in the least amount of turns. I don't think that this is that big of a sacrifice and can easily be adjusted after I calculate the best strategy.

Here is the biggest compromise I had to make in order to solve the problem: In the real game you can pick which scoring dice you will set aside but in my game you have to set aside all the scoring dice. If your first throw were {1,5,2,2,3,3} you cannot just set aside the 1 and throw remaining five dice, you have to set aside 1 and 5, then throw the remaining four dice. After all I am not trying to create an unbeatable AI, I am just trying to find a strategy that can guide people while playing the game. 

This seems easy enough

My first instinct was to just calculate the expected value for a $n$ dice throw like I did in my blackjack game. Expected value, intuitively, is the average score you get when you play the game infinitely many times.  The formal definition is:

Let $X$ be the finite list of all possible outcomes $\{x_1, x_2,...,x_n\}$ where all outcomes respectively have the probability $\{p_1, p_2,...,p_n\}$. Then the expected value is defined as 

\[E[X]=x_1 p_1 + x_2 p_2 + ... + x_n p_n\]

If you want more more information on the expected value click here or here. 

It was impossible for me to calculate the expected value given a dice throw by hand since there were so many possibilities.  So I wrote a small program which calculated it for me. Basically a function took the average of all possible points for an $n$ dice throw. Here are the results:

Expected value of an $n$ Dice Throw

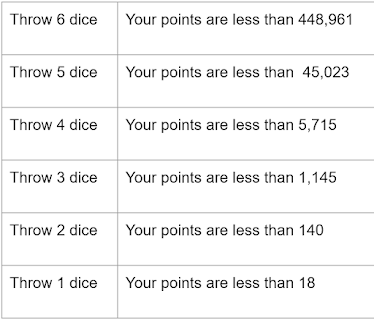
So for example if you were to throw three dice over and over again the average score you got on your throw would be approximately 93.75. Then I, and by "I" I mean the computer, calculated the possibility of a bust given a dice throw. Here are the results:

Probability of a Bust of an $n$ Dice Throw

After these findings my strategy was ready: Let's say you want to decide whether to bank your accumulated points or roll $n$ dice. If your points are more than what we expect to gain from the throw, then we should bank; roll otherwise. Let $P$ denote our points, $B$ our bust possibility and naturally $1-B$ our non bust possibility. Here is how we calculate when to throw:

\[P< (P+E) \times (1-B) + 0 \times B \]

\[P< P + E -BP -EB\]

\[BP< E \times (1-B)\]

\[P< \frac{E \times (1-B)}{B} \]

Then we got this graph:

WRONG Strategy

Can you see where I went wrong? When I looked at this graph, I felt confused. It was clearly wrong. Then it hit me. 

My expected values were wrong. Your 1 die throw's expected value has to be higher than 25 since if you roll a 5 or 1, you'll get back your 6 dice (and with those 6 dice the expected value is at least 487.).  But the framework was ready, all I had to do was to just calculate the true expected values, right?

Okay maybe this is difficult.

I started to see everything difficult about calculating the expected value. The amount of remaining dice changed so I couldn't just multiply everything with a non-bust probability. Worst of all it was recursive. I had to know the expected value of 6 in order to calculate the expected value of 1 and in order the calculate the expected value of 6 I had to know the expected value of 1! The game had the potential to take an almost infinitely long time. If this game had less amount of possibilities  I probably would be able to calculate it with pen and paper but there were just too many possibilities. I was about to give up, it was clear that I didn't know enough probability to solve this question. 

Then I had a second revelation. I didn't have to be exact. I just wanted to create a chart that people could look at in order to decide whether to roll or not. Do you remember the intuitive definition of an expected value? I was just going to simulate the game 1,000,000 times with different amount of dice in order to calculate the approximate expected values. Thank god for computers, coming to my rescue when I can't solve a question on my own. Here are the approximate expected values:

Approximate Expected Values

So here is your cheat sheet while playing the game Farkle in Kingdom Come Deliverance:

The Correct Strategy

Of course this game is much more than this. I just tried to make a simple mathematical guide. After I take a probability course, I'll probably try to calculate the real expected value but for now this is good enough. Have fun playing.